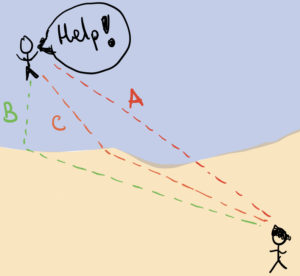
Let us consider the following scenario: on a sunny day, some people decide to go to the beach and have some fun with the waves. A coastal guard is keeping an eye on the swimmers, and she notices that one of them appears to be drowning. To help the person in distress, she has to decide which path will take her to the swimmer in the least amount of time: she could try to get to there in a straight line (path A), but in this case she would have to swim most of the way. Alternatively, she could run a lot on the sand and swim the least amount of distance (path B). However, even though humans run faster than they can swim, the most efficient way to get to the surfer is making a compromise the amount of running on the sand and swimming on the water (path C).
Light behaves in this way too. When it has to go from a point $A$ to another point $B$, it will take the path that guarantees the least amount of time, and such a path, as in the case of the coast guard, may not be a straight line. Because of this, when we put a straw in a glass of water, it looks like the straw is bending. Well, it is actually the light that is bending!
While the concept of light bending was known by the ancient Greeks, it was not until the enlightenment that the description was put in mathematical terms. Willebrord Snellius showed that the relation between the angles with which light approaches the interface in one medium and leaves the interface in the other medium are related as $$\frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2}\,,$$ where $v_1$ and $v_2$ are the velocity at which light propagates on each of the media. As nothing can travel faster than the speed of light in vacuum, it is convenient to define the velocity of propagation of light in a given medium as $v=c/n$, where $n$ is the so-called index of refraction of the medium. Thus, the relation above becomes $$\frac{\sin \theta_1}{\sin \theta_2} = \frac{n_2}{n_1}\,,$$ which is the well-known Snell’s law.
Armed with this equation, we may tackle more involved problems, as the refraction of light when the interface between the two media is spherical, as shown in the figure below.
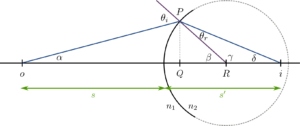
From the sketch becomes reasonable that an object placed in the medium with refraction index $n_1$ will generate an image (is it real or virtual?) on the medium with refraction index $n_2\,.$ The problem is as fundamental as it gets: we need to find the relation between the position of the object $o$, the position of the image $i$, the radius of the spherical surface $R$ and the refraction of the two media $n_1$ and $n_2$.
Let us consider a ray of light that goes from the position of the object $o$, to an arbitrary point $P$ on the spherical surface. The light impinges onto the surface at an angle $\theta_i$, as measured from the line perpendicular to the surface (shown in purple on the sketch). When passing to the medium with refraction index $n_2$, the light refracts and leaves the surface at an angle $\theta_r$ (from the sketch, does $n_2<n_1$ or $n_1<n_2$?), and continues its propagation until it reaches the optical axis.
Considering that the sum of the angles inside of a triangle is equal to $\pi$, we know that the angles in the sketch are related as follows:
- $\delta + \gamma+\theta_r=\pi$.
- $\beta+\gamma=\pi$.
- $\alpha+\beta+(\pi-\theta_i)=\pi$.
Using 1. and 2. get can get rid of the angle $\gamma$ to find $\theta_r=\beta-\delta$, and simplifying 3. we have $\theta_i = \alpha+\beta$.
Conversely, we know that
$$\tan \alpha = \frac{PQ}{oQ}\,, \quad \quad \tan \delta = \frac{PQ}{Qi} \quad \quad \mathrm{and} \quad \quad \tan \beta = \frac{PQ}{QR}\,,$$
where, for instance, $PQ$ is the distance between the points $P$ and $Q$. Furthermore, in the paraxial approximation, in which we assume that the rays are barely separated from the optical axis, we have very smalls angles an therefore: $\tan \alpha \approx \alpha$, $\tan \delta \approx \delta$, $\tan \beta \approx \beta$, $\sin \theta_i \approx \theta_i$, $\sin \theta_r \approx \theta_r$ and notably $oQ \approx s$, $Qi \approx s’$ and $QR \approx R$ . Using these approximations we have the following equations:
- From Snell’s law we have: $n_1 \theta_i = n_2 \theta_r$.
- The relation $\theta_r=\beta-\delta$ becomes $\theta_r = \frac{PQ}{R} – \frac{PQ}{s’}$.
- The relation $\theta_i = \alpha+\beta$ becomes $\theta_i = \frac{PQ}{s}+\frac{PQ}{R}$.
Joining these three equations we obtain
$$n_1 \left( \frac{PQ}{s}+\frac{PQ}{R} \right) =n_2 \left(\frac{PQ}{R} – \frac{PQ}{s’} \right)\,.$$
Dividing the two sides by the distance $PQ$ and rearranging the terms, we get
$$ \frac{n_1}{s} + \frac{n_2}{s’} = \frac{n_2-n_1}{R}\,,$$
which is the final form of our relation.