2018 marks the 400th anniversary of Kepler’s laws (I’m not sure that many know about this birthday). In Harmonices Mundi, the Dutch physicist reported a great discovery (his third law). It states that:
The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
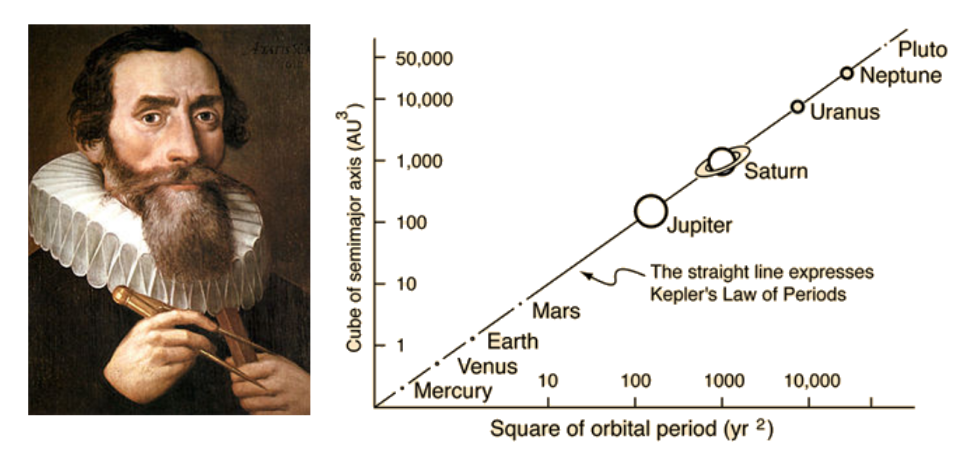
This resulted from many observations and a lot of fiddling with numbers (allegedly stolen from Tycho Brahe), until this mysterious relationship was discovered, a feast which impressed Einstein himself. The delight of the discovery was penned by the author of the harmonies of the world in a way unfortunately not available nowadays to scientific publications:
I first believed I was dreaming… But it is absolutely certain and exact that the ratio which exists between the period times of any two planets is precisely the ratio of the 3/2th power of the mean distance.
It was a bit strange and as most people who come with something genuinely new, poor Kepler met with much criticism. His own mentor (some now-forgotten Michael Mästlin) objected to him that “One should only treat astronomical things astronomically and not mix them with earthly physics.” The greatest breakthrough in Physics, Newton’s Universal theory of gravitation, would precisely show that Physics is what mixes earthly things like falling apples with astronomical ones like the falling moon.
We used this example during induction week as an illustration of the difference between an empirical law (Johannes’ observation cooked up into three particular laws) and a theoretical model (Newton’s theory expressed into three general and far-reaching laws). Another example we discussed is Rydberg’s formula and Bohr model of the atom, to explain the spectral lines of hydrogen.
How Newton derived Kepler’s law is a topic in Mechanics. Two of our students already knew the trick, and could reconstruct it… during the lecture! This is the note handed over by Luke after the class:
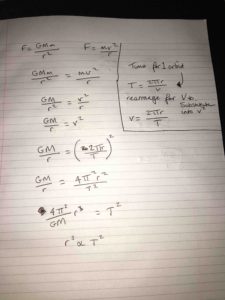
Well done! And came another, more detailed derivation from Joel, which went along the same line. To have something new to show, we asked Joel to compute the numerical value of Kepler’s constant in SI units (which we also covered) and this is what he found

That is, 7.52 MAU$^3$/day$^2$ (MAU is Mega-Astronomical units), vs 7.51 for Kepler’s average over six planets. These are the units from the Wikipedia (as also used by Kepler). They should really be in Mau$^3$/year$^2$ in which case the number is much more meaningful in itself (and is not exactly 1 for Earth, do you see why? We have a comment section if you want to contribute your thoughts).
Planetary motion will definitely make several comebacks in our Mechanics course, taught by an astro-solar-mathematico-physicist, and so will Rydberg’s formula, although it is not until the end of Year 5 that the connection will be established in this case (and so far we did not receive any back-of-the-envelope derivation for that). It’s also my birthday today, so I’ll leave the connection between empirical observations and theoretical models at that for today.
