Hall effect

The Hall effect
Introduction
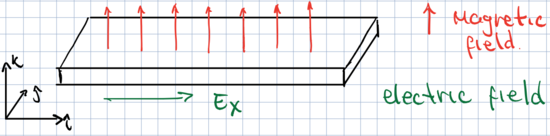
When an electrical current flows through an electrical conductor and a magnetifc field is applied transversally to the current, one observes the appearance of a potential difference (commonly referred to as the Hall voltage $V_H$).
The motion of electrons on the conductor, in the presence of impurities (with a finite collision time) is given by \begin{equation} \label{eq:force1} \mathbf{F} = m \left (\frac{d}{dt} + \frac{1}{\tau} \right) \mathbf{v}\,, \end{equation} where $m$ is the mass of the electron, $\tau$ is the mean collision time (i.e., the average time during which electrons can travel before colliding with something else), and $\mathbf{v}$ is the velocity with which the electrons move.
- the term $m d\mathbf{v}/dt$ describes the free acceleration,
- the term $m\mathbf{v}/\tau$ describes the effect of the collisions, which in practice acts as a friction.
In the presence of an electromagnetic magnetic field, the electrons experiment Lorentz force, namely we have \begin{equation} \label{eq:force2} \mathbf{F} = m \left (\frac{d}{dt} + \frac{1}{\tau} \right) \mathbf{v} = -e \left (\mathbf{E} + \mathbf{v} \times \mathbf{B}\right)\,, \end{equation} where $\mathbf{E}$ and $\mathbf{B}$ are the electric and magnetic fields acting on the electric conductor.
In teh steady state, when then velocity of the electons is constant in time (thus reaching the so-called drift velocity), Eq. (\ref{eq:force2}) becomes \begin{equation} \label{eq:DriftVelocity} \mathbf{v} = - \frac{e\tau}{m} \left (\mathbf{E} + \mathbf{v} \times \mathbf{B}\right)\,. \end{equation}
Let's consider a particular case, in which the magnetic field is given by $\mathbf{B} = B \mathbf{z}$, where $\mathbf{z}$ is the unit vector along the z-axis. In this case, $\mathbf{v}\times \mathbf{B} = (B v_y, -Bv_x,0)$ and Eq. (\ref{eq:DriftVelocity}) becomes \begin{align} v_x & = -\frac{e\tau}{m} E_x - \frac{Be\tau}{m}\,,\\ v_y & = -\frac{e\tau}{m} E_y + \frac{Be\tau}{m}\,,\\ v_z & = -\frac{e\tau}{m} E_z \end{align} Let's now assume that we apply an eletic field along the x-axis:
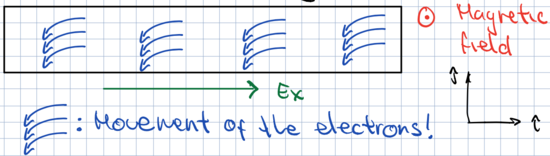
Because the electric field $E_x$ induces an electric current along the x-axis. This current is transverse to the magnetic field, and therefore the electrons move as sketched below (seen from above the sample)
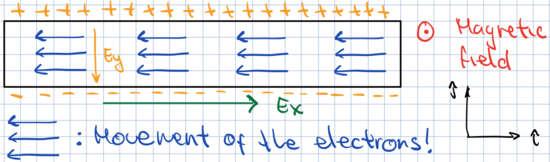
The electric field will induce a motion on the electrons, which will be diverted towards the edge by the magnetic field. However, since electrons cannot scape the conductor, they accumulate on its edges, thus induing an electric field along the y-axis, $E_y$.
This induced electric field is such that it counteracts the effect of the magnetic field on the electrons, which now can travel in straight lines. In other words, $E_y$ is such that $v_y=0$. Introducing this condition on the equations above, we find that the induced electric field is \begin{equation} \label{eq:InducedEy} E_y = - \frac{Be\tau}{m} E_x\,. \end{equation} and that the drift velocity along the x-axis is $v_x = -(e\tau/m) E_x$.
Using Ohm's law we can relate the density of current $\mathbf{J}$ and the electric field $\mathrm{E}$ \begin{equation} \label{Eq:OhmLaw} \mathbf{J} = \sigma \mathbf{E} = \left( \frac{ne^2 \tau}{m} \right) \mathrm{E}\,, \end{equation} where $\sigma$ is the conductivity of the conductor and $n$ is the density of charge carriers in the sample. Therefore, we have that $E_x = m J_x/(n e^2 \tau)$ and \begin{equation} E_y = -\frac{B}{n e} J_x\,, \quad \quad \mathrm{and} \quad \quad v_x = - \frac{1}{ne}J_x = \frac{E_y}{B}\,. \end{equation} Finally, if the dimensions of the sample are $b$, $d$, $w$ along the x-, y-, and z-axis, respectively, we have that the applied current $I$ along the x-axis is $I=J_x/(b d)$ and the potential infuced by the electric field along the y-axis is $V_H= E_y/b$. Replacing the field and density of currents, we find \begin{equation} V_H = - \frac{B}{n e d} I\,, \quad \quad \mathrm{and} \quad \quad v_x = - \frac{1}{ne}J_x = \frac{V_H}{bB}\,. \end{equation}
Procedure
Constant magnetic field
In this part of the experiment, the magnetic field will be held constant and the current through the semi-conductor will be varied.
- Set the Excitation Current $(I_M)$ 0-1000 mA to a desired value (e.g., 500 mA) so the magnetic field strength will be constant.
- Make sure the Hall Current $I_s$ 0-10mA is zero.
- Click Preview and adjust the Hall Current to 0.5 mA. Press Keep to record the voltage and current. Then increase the Hall Current by increments of 0.5 mA, pressing Keep for each, until the Hall Current is 5.5 mA. Then press Stop. Return the Hall Current to zero.
- Move the Hall Probe out of the magnet. Press the tare button on the side of the Magnetic Field Sensor. Move the end of the Magnetic Field Sensor into the center of the magnet. Click Preview and Keep to record the magnetic field strength. Then press Stop.
- Set the current 0-1000mA to another value (e.g., 800 mA), and then record data again, repeating Steps 2 through 4.
- Hall Voltage Compensation: Because the leads that measure the Hall Voltage may not be exactly opposite each other across the semi-conductor, a voltage may appear that is due to the potential difference along the direction of the current. To measure this and compensate for it, slide the Hall Probe completely out of the magnet, set the magnet current to zero, and perform Step 3 to record the Hall Voltage without any magnetic field. Apply a linear fit to the V vs. I data. The slope of this line will be subtracted from the slopes of the other lines to compensate for the offset of the Hall Voltage due to misalignment of the leads.
Constant Current through the Semi-Conductor
In this part of the experiment, the magnetic field will be varied by varying the current through the electromagnet while the current through the semi-conductor will be held constant. Rather than measuring the magnetic field for each data point, we will first characterize the magnetic field as a function of the current.
- To discover the relationship between the magnetic field strength and the current through the magnet coils, create a table of Magnetic Field Strength (Perpendicular). In the second column, create a User-Entered data set called Magnet Current (with units of mA). Pre-fill the column with values from 50 to 900 mA in steps of 50 mA. Create a graph of Magnetic Field Strength (Perpendicular) vs. Magnet Current (A).
- With the Hall Current set to zero, press the tare button on the side of the Magnetic Field Sensor. Move the Magnetic Field Sensor into the center of the magnet.
- Click Preview and adjust the “Excitation Current” (the current through the electromagnet) to 50 mA as read on the digital readout on the Hall Effect Apparatus. Then click Keep.
- Adjust the “Excitation Current” to each value in the table and click Keep for each value. Then click Stop. Return the Excitation Current to zero to prevent the magnet from getting too hot.
- On the graph, apply a cubic curve fit.
- Set the Hall current $I_s$ (0-10 mA) to a desired value (e.g., 5 mA).
- Make sure the Excitation Current $(I_M)$ 0-1000 mA is zero.
- Set the sampling rate to 10 Hz.
- Move the Magnetic Field Sensor out of the magnet and move the Hall Effect Probe into the center of the magnet.
- Click Preview and increase the Excitation Current to 50 mA and click Keep. Continue to increase the Excitation Current by steps of 50 mA up to 900 mA, clicking Keep for each current setting. Then click Stop. With the fit done in step 5, you can deduce the magnetic field produce at every value of the current.
- Set the Hall Current 0-10 mA to another value (e.g., 8 mA), then record data again,
repeating Steps 7 through 10.
Results & analysis
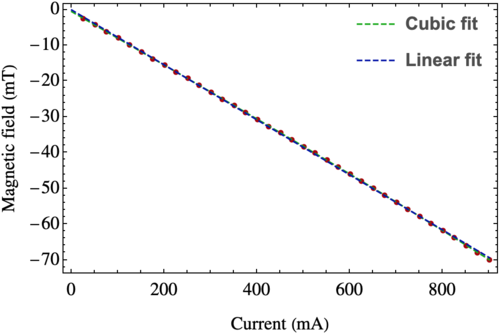
Magnetic field as a function of the current
The results of the measurement are displayed in the figure below.
There, we can make a cubic fit (as recommended by the manufacturer) or a linear fit. Which one is better? The parameters of the fit with $B=a_0 +a_1 I + a_2 I^2 + a_3 I^3$ are the following:
| Fit | $a_0\, (\mathrm{mT})$ | $a_1\, (\mathrm{mT}/\mathrm{mA})$ | $a_2\, (\mathrm{mT}/\mathrm{mA}^2)$ | $a_3\, (\mathrm{mT}/\mathrm{mA}^3)$ |
|---|---|---|---|---|
| Linear | -(1.17 $\pm$ 0.87)$\times 10^{-1}$ | -(7.70 $\pm$ 0.01)$\times 10^{-2}$ | - | - |
| Cubic | -(5.88 $\pm$ 0.28)$\times 10^{-1}$ | -(7.48 $\pm$ 0.03)$\times 10^{-2}$ | (2.01 $\pm$ 0.64)$\times 10^{-7}$ | -(3.05 $\pm$ 0.45)$\times 10^{-9}$ |
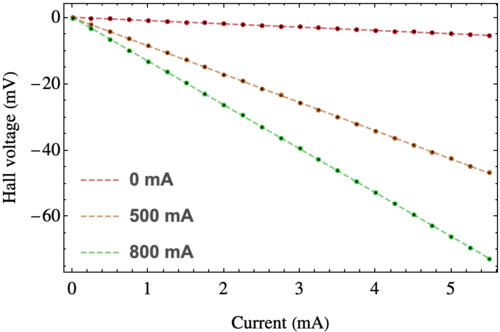
Hall voltage at fixed magnetic field
The results of the measurement are shown in the figure below (note that the error bars are within the size of the dots!).
The data can be linearly fitted, i.e., with an expression as $V_H = a_0 + a_1 I$, with the following parameters:
| Current (mA) | $a_0\, (\mathrm{mV})$ | $a_1\, (\mathrm{mV}/\mathrm{mA})$ |
|---|---|---|
| 0 | (0.156 $\pm$ 0.010) | -(0.993 $\pm$ 0.003) |
| 500 | (0.019 $\pm$ 0.023) | -(8.529 $\pm$ 0.007) |
| 800 | (0.114 $\pm$ 0.033) | -(13.220 $\pm$ 0.011) |
From the measurement of the magnetic field as a function of the current in the coils, done in the previous section, we know that the magnetic fields corresponding to 500 mA and 800 mA are $-(38.59 \pm 0.13)\,\mathrm{mT}$ and $-(61.68 \pm 0.14)\,\mathrm{mT}$, respectively. The Hall voltage is related to the current $I$ passing through the semiconductor with the follwoing expression \begin{equation} \label{eq:hallvoltage} V_H = -\left(\frac{B}{nde} \right) I = -\left (\frac{R_H B}{d} \right) I\,, \end{equation} where $B$ is the magnetic field, $n$ is the density of charge carriers in the semiconductor, $d$ is the depth of the semiconductor sample and $e$ is the charge of the electron. We have also defined $R_H = 1/(ne)$, known as the Hall coefficient, which depends on the material and the temperature, but is independent of the geometry of the sample. With the data collected and having that $d=1.2\,\mathrm{mm}$, we find that the Hall coefficient of the semiconductor of the setup is $R_H = (0.2361 \pm 0.0005)\,\mathrm{m}^3/C$, and therefore the density of charge carriers on the sample is $n=(2.6438 \pm 0.0006)\times 10^{19}\,\mathrm{m}^{-3}$.
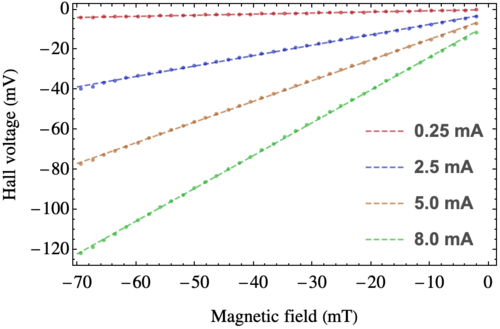
Hall voltage at fixed current through the sample
The results of the measurement are shown in the figure below (note that the error bars are within the size of the dots!).
The data can be linearly fitted, i.e., with an expression as $V_H = a_0 + a_1 B$, with the following parameters:
| Current (mA) | $a_0\, (\mathrm{mV})$ | $a_1\, (\mathrm{mV}/\mathrm{mA})$ |
|---|---|---|
| 0.25 | -(0.077 $\pm$ 0.010) | (0.0556 $\pm$ 0.0003) |
| 2.5 | -(2.179 $\pm$ 0.085) | (0.521 $\pm$ 0.002) |
| 5.0 | -(4.474 $\pm$ 0.113) | (1.035 $\pm$ 0.003) |
| 8.0 | (7.334 $\pm$ 0.122) | (1.639 $\pm$ 0.003) |
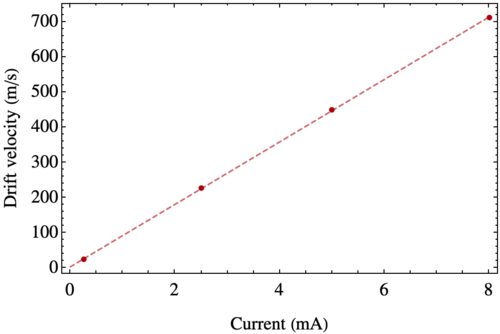
From the slope and using Eq. (\ref{eq:hallvoltage}) we can deduce that the Hall coefficient is $R_H = (0.2527 \pm 0.0005)\,\mathrm{m}^3/C$, and therefore the density of charge carriers on the sample is $n=(2.4697 \pm 0.0004)\times 10^{19}\,\mathrm{m}^{-3}$, which are similar values to the ones obtained in the previous section. On the other hand, the relation betwenn the Hall voltage and the magnetic field can also be written as \begin{equation} V_H = b v B\,, \end{equation} where $b=2.3\,\mathrm{mm}$ is the base of the sample and&nbps;$v$ is the drift velocity with which the charge carriers move through the sample. Solving for the latter, we find the follwing relation
| Current (mA) | $v\, (\mathrm{m}/\mathrm{s})$ |
|---|---|
| 0.25 | (24.15 $\pm$ 0.11) |
| 2.5 | (226.54 $\pm$ 0.93) |
| 5.0 | (449.86 $\pm$ 1.24) |
| 8.0 | (712.82 $\pm$ 1.34) |
These points lie on a straight line, as shown in the figure below.
From which we can predict that if a current $I$ (in mA) flows through the sample, the drift velocity of the carriers will be \begin{equation} v = (3.41 \pm 1.88) + (88.87 \pm 0.39) I\,. \end{equation}