Our Matrix Quiz for the Ray Matrices module had this entry:
Multiply two matrices for thin lenses, with focal lengths
and
. What do you find? What does this tell you about this compound lens?
Canvas actually allows you to typeset your answer but we cover $\LaTeX$ in 2nd semester, so we have to deal with ASCII tricks, but that doesn’t matter. What does is the answer, which is here correctly given by Dilem:
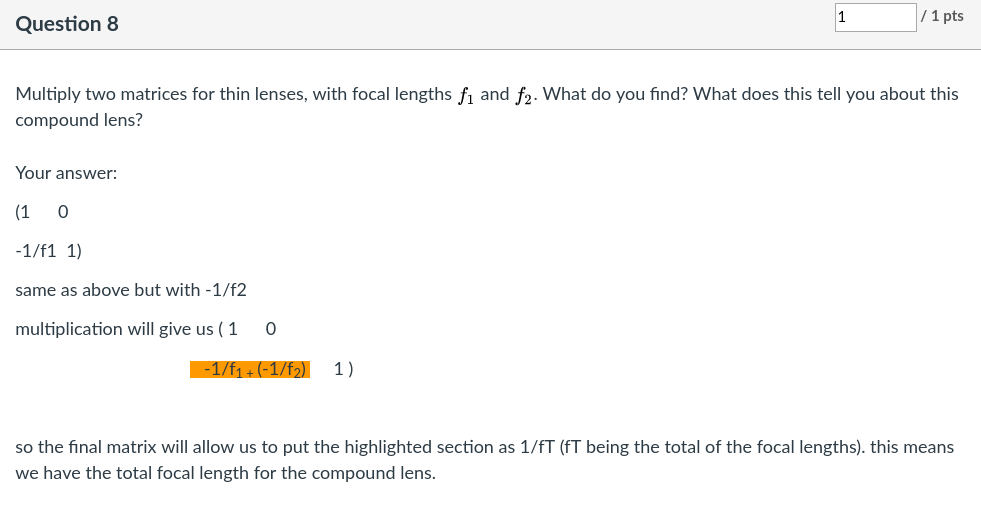
I have little to add. This is another basically correct entry, with a more loose articulation of the conclusion (“focal length equal to the sum of each lens“):

These are less successful or less inspired entries:
It’s dependent on the focal length
As the focal length is here in the singular, maybe it is meant that the compound object depends on its focal length. It sounds like a tautology, or a trivial statement. It looks like the student just tried a desperate reply that sounds like the sort of answer that could grab a few points (it did get 0.25 as it’s not clearly incorrect).
They magnify
Who is “They”? The compound lens could, or not, magnify. I think this has missed the point (which was to recognize that the compound object behaves as a lens, in the first place).
(1 , -1/f2) (-1/f1, -1/f1 x -1/f2 +1) I have no idea what this tells me
Here there seems to be some error in the computation, doubled with some confusing notation. No wonder this is totally unclear what this could tell. At least the student recognizes it’s unclear rather than making a mystifying statement that would convey the impression they have a clever idea.
The matrice for a compound lense is only reliant on -1/f
Another unclear—trying-to-guess-what-answer-could-work—statement. It could be interpreted as correct, with the implication that the compound object is a lens fully determined by its focal length, which also looks a tautology, also, $f$ is not clearly defined. So unless you know the answer, I believe it’s difficult to make much sense out of this input. Quarter of a point.
And the most popular reply:
We indeed got 2 students who left this entry blank (out of those who took the Quiz in time).
This is the reasoning (adapted from our Canvas module). The matrix of a compound lens formed by putting two thin lenses back to back is given by the product of their ray matrices:
$$M_{f_1}M_{f_2}=\begin{pmatrix}1&0\\\displaystyle-\frac1f_1&1\end{pmatrix}
\begin{pmatrix}1&0\\\displaystyle-\frac1f_2&1\end{pmatrix}=\begin{pmatrix}1&0\\\displaystyle-\frac1f_1-\frac1f_2&1\end{pmatrix}$$
We can write this in a more economical but also more insightful form:
$$M_{f_1}M_{f_2}=M_{f_1f_2/(f_1+f_2)}$$
What the notation highlights is precisely the fact that the product matrix has the same form as each indivual matrix, therefore, the compound object behaves collectively as any of its single part. So two thin-lenses put back to back make another thin lens! The only obvious difference is that we now have a more involved expression for the $C$ element of the $ABCD$ matrix, but this we can always write as $-1/f_\mathrm{compound}$, and this gives us, furthemore, an expression for the compound focal length:
$$f_\mathrm{compound}=\displaystyle\frac{f_1f_2}{f_1+f_2}$$
What would have been great is an analogy to similar results familiar to the students from other fields, something like:
Focal lengths of thin lenses add like resistances put in parallel in an electric circuit.
And this observation would lead to further questions: is there a way to assemble lenses so that their focal lengths add like “in series” ($f_1+f_2$)? The fact lenses behave in this way is why we introduce the notion of vergence of optical systems. That’s maybe close to what Dylan had in mind, but he didn’t pursue it any further, I believe because of the imprecision of his formulation. A proper statement often opens natural new questions of its own, and when such a process is started, one is not merely answering a quiz on Canvas, but is doing research already…
