Dressed states

The dynamics of a coherently driven two-level system (2LS) is described through the Hamiltonian (in the frame rotating with the frequency of the laser, and setting $\hbar=1$) \begin{equation} \label{eq:WedJul19121758CEST2017} H = (\omega_\sigma-\omega_\mathrm{L}) \sigma^\dagger \sigma + \Omega (\sigma + \sigma^\dagger)\,. \end{equation} Here $\sigma = |g\rangle \langle e|$ is the operator that lowers the state of the 2LS, $\omega_\sigma$ is the frequency of the 2LS and $\omega_\mathrm{L}$ is the frequency of the laser that drives the 2LS with intensity $\Omega$.

Turning to the basis of the dressed states of the 2LS: \begin{equation*} |+\rangle = \sin \theta |g\rangle + \cos \theta |g\rangle\,, \end{equation*} \begin{equation*} |-\rangle = \cos \theta |e\rangle - \sin \theta |e\rangle\,, \end{equation*} the Hamiltonian in Eq. (\ref{eq:WedJul19121758CEST2017}) becomes \begin{multline} \label{WedJul19123312CEST2017} H = |+\rangle\langle+| (\Delta \cos^2\theta+2\sin\cos\Omega) + |+\rangle\langle+| (\Delta \cos^2\theta-2\sin\cos\Omega)+\\ (|+\rangle\langle-| + |-\rangle\langle+|) [\Omega(\cos^2\theta - \sin^2\theta) -\Delta \sin\theta \cos\theta]\,, \end{multline} where $\Delta=\omega_\sigma-\omega_\mathrm{L}$.

The idea of the dressed states is to obtain a diagonal Hamiltonian, so we choose the angle $\theta$ in such a way that the term describing the coupling in Eq. (\ref{WedJul19123312CEST2017}) vanishes: \begin{equation} \label{WedJul19123636CEST2017} \Omega(\cos^2\theta -\sin^2\theta) -\Delta \sin\theta \cos\theta=0\,. \end{equation} Assuming that we can write \begin{equation*} \cos^2\theta=\frac{x^2}{1+x^2} \quad \mathrm{and} \quad \sin^2\theta=\frac{1}{1+x^2}\,, \end{equation*} the condition in Eq. (\ref{WedJul19123636CEST2017}) yields \begin{equation} \label{eq:WedJul19130256CEST2017} x=\frac{\Delta + \sqrt{\Delta^2+4\Omega^2}}{2\Omega}\,. \end{equation}

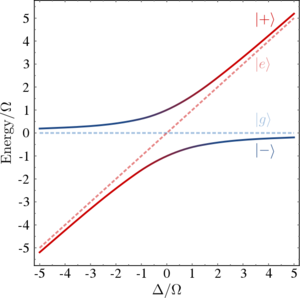
Fig. 1: Energy anticrossing as seen through the dressed states $|+\rangle$ and $|-\rangle$.

With this value, the Hamiltonian describing the 2LS is simply by $H=E_+ |+\rangle\langle+| + E_{-} |-\rangle\langle-|$, where \begin{equation*} E_+=\frac{1}{2}\big( \Delta + \sqrt{\Delta^2+4\Omega^2}\big)\,, \end{equation*} \begin{equation*} E_-=\frac{1}{2}\big( \Delta - \sqrt{\Delta^2+4\Omega^2}\big)\,. \end{equation*} Figure 1 shows in solid lines the anticrossing of the energies of the dressed states as a function of the detuning between the 2LS and the driving laser. The bare states, $|g\rangle$ and $|e\rangle$, are shown in dashed light lines. The energy difference between the dressed states is given by $\sqrt{\Delta^2+4\Omega^2}$, which is commonly known as the Rabi splitting. The minimum splitting is obtained at resonance and $E_+-E_- = 2\Omega^2$.